LaTeX Math

Overview

Teaching: 0 min
Exercises: 0 min

Questions

• How do I use equations in LaTeX?

Objectives

• Explain the way to activate math mode in-line and as an environment

• Render sample math text in LaTeX

• Learn how to represent some common symbols with math

• Apply superscripts, subscripts, and similar symbolic nomenclature

• Learn how to to properly employ braces

• Create fractions properly

• Align equations over multiple lines

• Break a long equation across multiple lines

One of the most powerful parts of LaTeX is its ability to properly typeset mathematical equations. The groundwork TeX laid for typesetting equations is so important, that nearly every writing tool that even attempts to make math look “correct” uses TeX at its core.

Math Mode

Math mode is an environment which can be called in LaTeX. It changes the typesetting from a focus on readable text to treating characters entered as mathematical variables and operators. The logic is very simple, and can be used to create very complex notation.

Math mode ignores spaces.

The math mode environment can be called in several ways. The first, and most obvious, is by creating an equation environment.

\documentclass{article}
\begin{document}
  What is y?
  \begin{equation}
      y = 3x+21
  \end{equation}
\end{document}

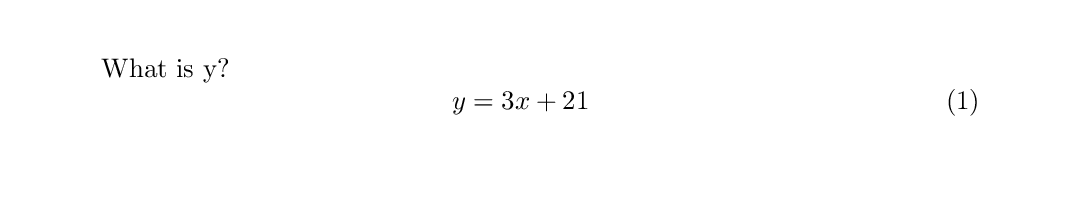
The equation environment not only enters math mode, but also prints the equation number in the righthand margin, as is required in many mathematical contexts. If you do not want an equation number printed in the margin, the number will be ignored if we issue a “do not count” version of it using equation*. This command is provided by the amsmath package.

\documentclass{article}
\begin{document}
  What is y?
  \begin{equation*}
      y = 3x+21
  \end{equation*}
\end{document}

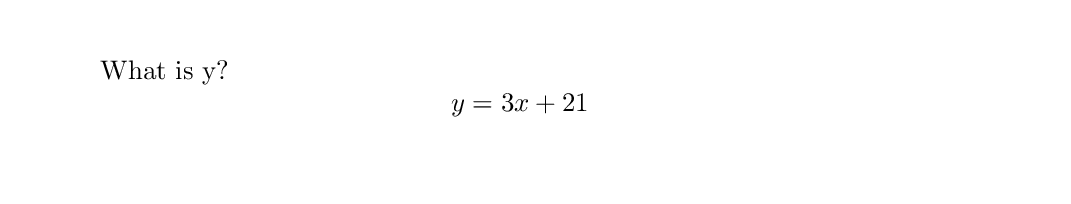
One synonym for the equation* environment is the square bracket environment. This has the exact same properties as equation*, but is called with a shorter command that does not require the amsmath package.

\documentclass{article}
\begin{document}
  What is y?
  \[
      y = 3x+21
  \]
\end{document}

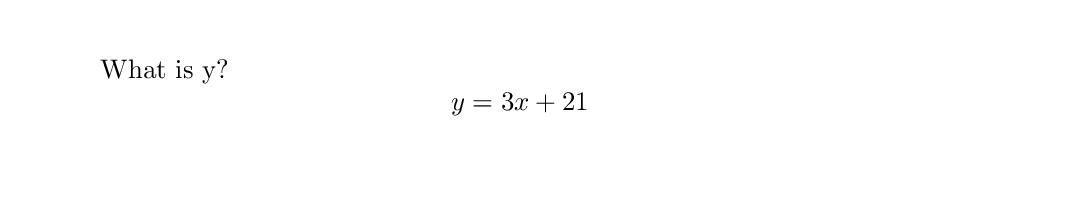
Inline Math

Often it is important to include some equation or even a single symbol within the body of text of a document. It is possible to enter into math mode using $ (without escape characters). While this will enter math mode, it will not increase an equation counter.

\documentclass{article}
\begin{document}
  What is $y$?
  \begin{equation}
      y = 3x+21
  \end{equation}
\end{document}

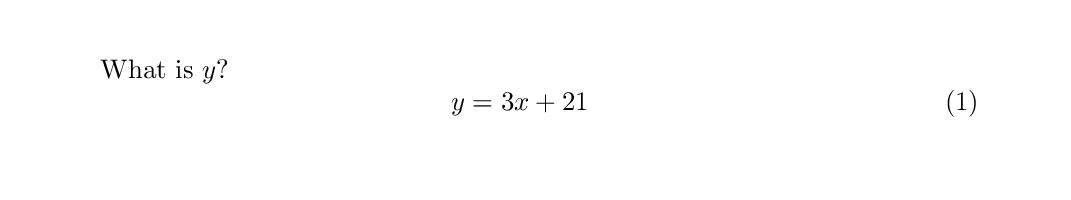
Super- and Sub- scripting

To begin entering notation within a superscript (e.g. a power function) or a subscript (e.g. the nth value in a series), the caret (^) or underscore (_) character is used, respecitvely. Any notation placed in curly braces at these commands will be shifted into this script level.

\documentclass{article}
\begin{document}
  What is $y_{n}$?
  \begin{equation}
      y_{n} = 3x^{2}+21
  \end{equation}
\end{document}

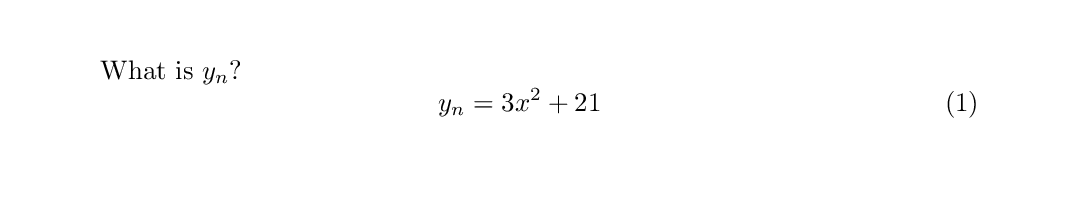
If no curly braces are used, the first character to follow the script symbol is promoted/demoted. This means that $x^2$ is a valid function, but $x^20$ would not equal $x^{20}$. It is wise to get in the habit of using curly braces all the time, to prevent confusion.

This scripting works with symbols too.

\documentclass{article}
\begin{document}
  What is the volume of a solid ($V$) with a non-uniform cross-sectional area ($A$)?
  \begin{equation}
      V = \int_{n_{1}}^{n_{2}}A(x)dx
  \end{equation}
\end{document}

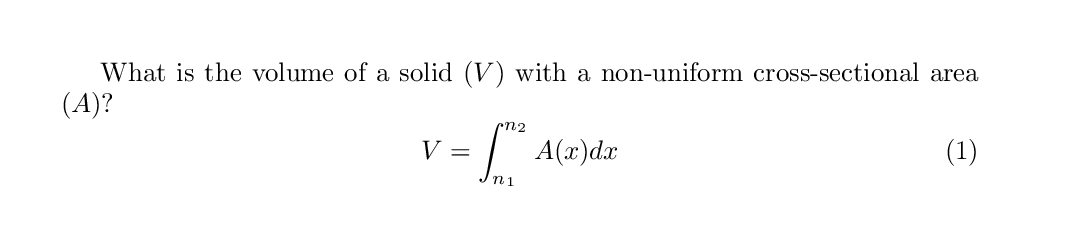
Stacking Fractions and Division

Plain text makes division notation look nothing like we might see in a good math textbook. This is also true when we enter math mode. The backslash / as a divisor just looks silly. Our math looks much better when stacked appropriately above and below a horizontal line. For this, we use the command frac, where the numerator and denominator go in sequential curly braces.

\documentclass{article}
\begin{document}
  What is slope ($m$)?
  \begin{equation}
      m = (y_{2}-y_{1})/(x_{2}-x_{1})
  \end{equation}
  ~
  \begin{equation}
      m = \frac{y_{2}-y_{1}}{x_{1}-x_{2}}
  \end{equation}
\end{document}

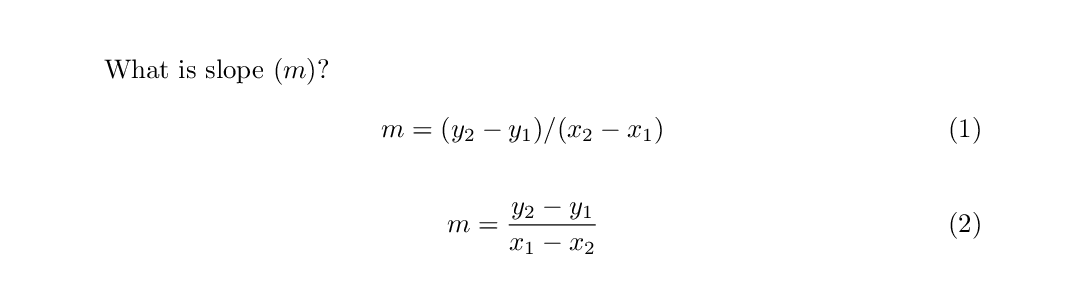
Dynamic Delimiters

While it may seem easy to use simple delimiters, such as parentheses in math mode, they do not operate the way one might expect. When a parenthesis is entered as notation, the size will be static and unchanging. However, the height of an equation when displayed in math mode is stretchy. It is recommended to use special delimiters such as left( and right) instead, as these will automatically adapt to the size of the rest of the notation within the environment.

\documentclass{article}
\begin{document}
  What is the attractive force of two bodies ($F$)?
  \begin{equation}
      F = G(\frac{m_{1}m_{2}}{r^{2}})
  \end{equation}
  ~
  \begin{equation}
      F = G\left(\frac{m_{1}m_{2}}{r^{2}}\right)
  \end{equation}
\end{document}

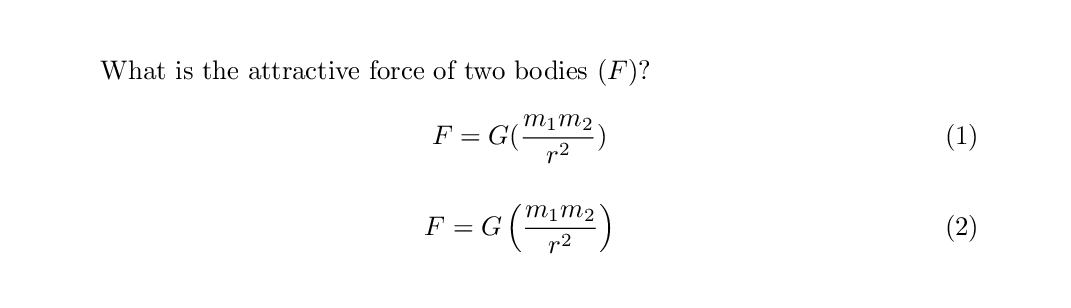
Even more delimiters are provided by the amsmath package, such as big ones (bigl() and some even bigger ones (Bigl()

What If I Need a Weird Symbol?

LaTeX is ready to accomodate your needs with many symbols. The default package comes with a large number of symbols which can be placed in math mode. They are all straightforward commands. No more will you have to hunt for ALT codes or copy and paste from the Unicode tables. The tables below list the symbols available to the default installation.

If you ever have a problem with a command sequence symbol not behaving next to a text symbol, such as \neqx not showing up properly, you can add a single set of curly braces to tell the LaTeX math parser not to confuse the separate entities (\neq{}x).

Breaking a Long Equation Across Multiple Lines

There are lots of ways to do this using the amsmath package, and we cannot cover them all here. Instead, we will focus on a few here.

Align Based on Centering Mark

Equations can be aligned across several lines which centers on a particular feature of an equation. The most common part of an equation to center is an equality. This is especially useful for multi-lined derivations. This can be performed with the align environment. Within this environment, equations will center wherever the user places an ampersand (&). Only one ampersand can be used for each line, and each line must be broken by a newline character (\\).

\documentclass{article}
\usepackage{amsmath}
\begin{document}
  Solve for a sphere:
  \begin{align}
    V &= \iiint \rho^{2} sin{\theta} d\rho d\theta d\varphi \\
    &= \int_{0}^{2\pi} \int_{0}^{\pi} \int_{0}^{r} \rho^{2} \sin{\theta} d\rho d\theta d\varphi \\
    &= 2\pi \int_{0}^{\pi} \int_{0}^{r} \rho^{2} \sin{\theta} d\rho d\theta \\
    &= 4\pi \int_{0}^{r} \rho^{2} d\rho \\
    &= \frac{4\pi}{3}\rho^{3}
  \end{align}
\end{document}

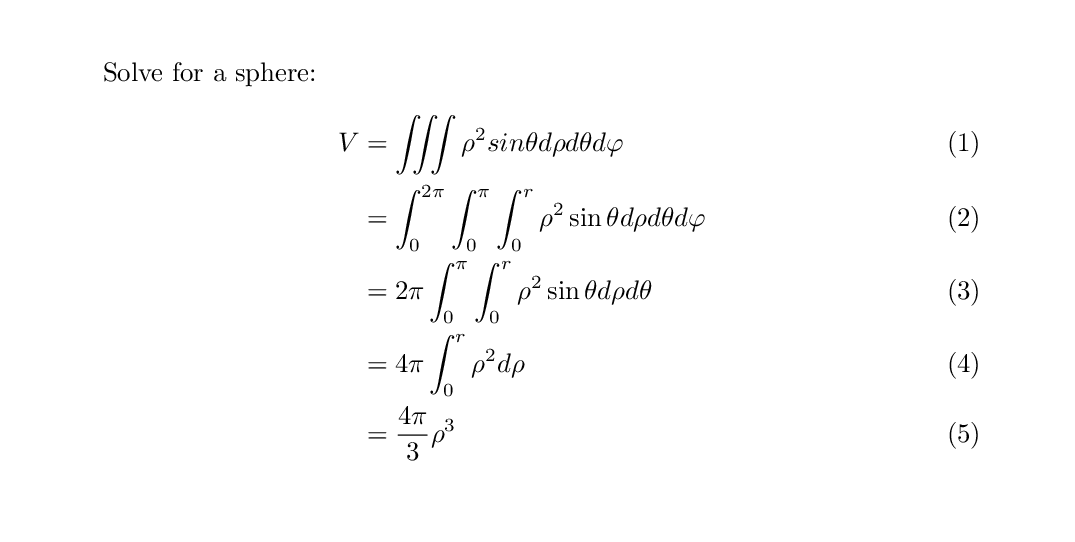
Note that each step in this equation is given an equation number counter. If we want everything in this equation block to have a single equation counter, we need to split a single align environment.

\documentclass{article}
\usepackage{amsmath}
\begin{document}
  Solve for a sphere:
  \begin{align}
    \begin{split}
      V &= \iiint \rho^{2} sin{\theta} d\rho d\theta d\varphi \\
      &= \int_{0}^{2\pi} \int_{0}^{\pi} \int_{0}^{r} \rho^{2} \sin{\theta} d\rho d\theta d\varphi \\
      &= 2\pi \int_{0}^{\pi} \int_{0}^{r} \rho^{2} \sin{\theta} d\rho d\theta \\
      &= 4\pi \int_{0}^{r} \rho^{2} d\rho \\
      &= \frac{4\pi}{3}\rho^{3}
    \end{split}
  \end{align}
\end{document}

The split is only a valid sub-environment for align. It can only be used within another float, not on its own.

As with most “counted” environments, align can be converted to align* to prevent adding a counter on the side of the page.

\documentclass{article}
\usepackage{amsmath}
\begin{document}
  Solve for a sphere:
  \begin{align*}
    \begin{split}
      V &= \iiint \rho^{2} sin{\theta} d\rho d\theta d\varphi \\
      &= \int_{0}^{2\pi} \int_{0}^{\pi} \int_{0}^{r} \rho^{2} \sin{\theta} d\rho d\theta d\varphi \\
      &= 2\pi \int_{0}^{\pi} \int_{0}^{r} \rho^{2} \sin{\theta} d\rho d\theta \\
      &= 4\pi \int_{0}^{r} \rho^{2} d\rho \\
      &= \frac{4\pi}{3}\rho^{3}
    \end{split}
  \end{align*}
\end{document}

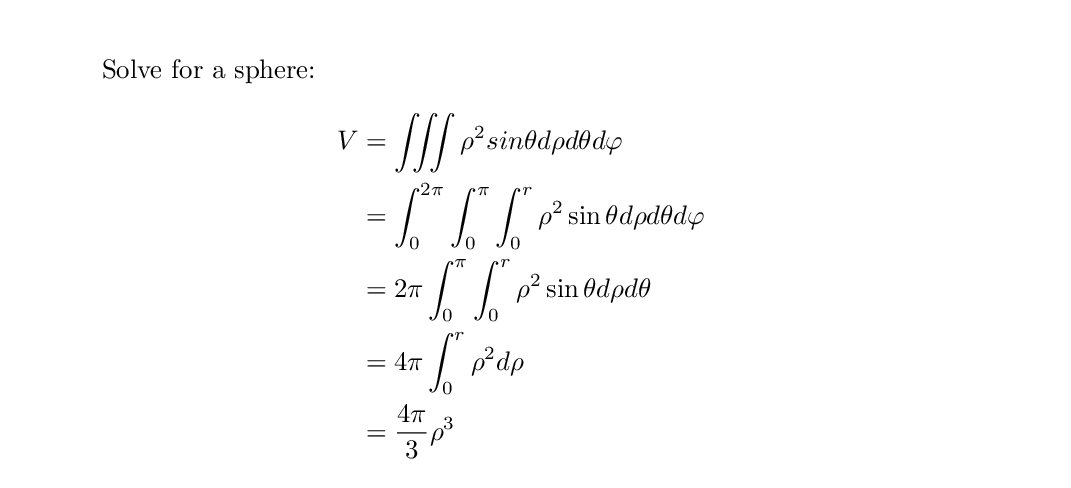
Adding Text Comments to Rendered Math

Sometimes, it is useful to add text to an equation without leaving the math environment. Text used in this case needs to distinctly be printed in the format as text from the body of a document, and not use math notation. To add text within an equation, use the text command within the math environment. This requires the amsmathpackage.

\documentclass{article}
\usepackage{amsmath}
\begin{document}
  What is the attractive force of two bodies ($F$)?
  \begin{equation}
      F = G\left(\frac{m_{1}m_{2}}{r^{2}}\right) \text{ Where } m_1 \text{ and } m_2
      \text{ are the mass of each body.}
  \end{equation}
\end{document}

Key Points

• Activate the math environment with equation

• Activate the in-line math mode with $

• Use the math environment without creating a numbered equation using equation* and []

• Enter Greek symbols such as phi with escape sequencies in math mode

• Distinguish super- and sub- levels of script with ^ and _

• Create an integral with int which is bound by text using ^ and _

• Recognize that mathematical symbols such as cos and sin must be escaped sequences

• Use left(, right(, and similar brace sequences to dynamically bound math

• Create fractions with the frac command instead of /

• Align a multistep sequence using the align and split environments using & helpers

• Include plaintext portions of aligned math using the array environment with &{} helpers

• Break a long equation up with multline